определение угла, измерение углов, обозначения и примеры

Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.

Определение угла

Определение 1

Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.

Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.

Определение 2

Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.

Иначе говоря, луч или

полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.

Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.

Перейдем к понятию определения угла.

Определение 3

Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.

Имеет место случай, когда стороны угла могут выступать в роли прямой линии.

Определение 4

Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой уго

Внутренний угол Википедия

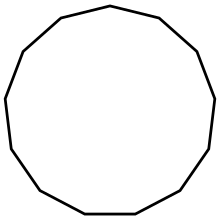Тринадцатиугольник — многоугольник с 13 углами и 13 вершинами.

Многоуго́льник — геометрическая фигура, обычно определяемая как часть плоскости, ограниченная замкнутой ломаной, звенья которой не пересекаются.

Варианты определений[ | ]

Многоугольники

Существуют три различных варианта определения многоугольника; последнее определение является наиболее распространённым.

• Плоская замкнутая ломаная — наиболее общий случай;
• Плоская замкнутая ломаная без самопересечений, любые два соседних звена которой не лежат на одной прямой;
• Часть плоскости, ограниченная замкнутой ломаной без самопересечений — плоский многоугольник; в этом случае сама ломаная называется контуром многоугольника.

В любом случае вершины ломаной называются вершинами многоугольника, а её звенья — сторонами многоугольника.

Связанные определения[ | ]

• Вершины многоугольника называются соседними, если они являются концами одной из его сторон.
• Стороны многоугольника называются смежными, если они прилегают к одной вершине.
• Отрезки, соединяющие несоседние вершины многоугольника, называются диагоналями.
• Углом (или внутренним углом) многоугольника при данной вершине называется угол, образованный его сторонами, сходящимися в этой вершине, и находящийся во внутренней области многоугольника. В частности, угол может превосходить 180°, если многоугольник невыпуклый.
• Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине. В общем случае внешний угол — разность между 180° и внутренним углом, он может принимать значения от −180° до 180°.

Виды многоугольников[ | ]

Теорема о внешнем угле треугольника — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 августа 2016; проверки требуют 9 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 августа 2016; проверки требуют 9 правок.

В геометрии внешним углом DCA плоского треугольника при данной вершине называется угол, смежный внутреннему углу ACB треугольника при этой вершине (см. рис.). Если внутренний угол при данной вершине треугольника образован двумя сторонами, выходящими из данной вершины, то

внешний угол треугольника образован одной стороной, выходящей из данной вершины и продолжением другой стороны, выходящей из той же вершины.

• Внешний угол равен разности между 180° и внутренним углом, он может принимать значения от 0 до 180° не включительно.
• Теорема о внешнем угле треугольника: Внешний угол треугольника равен сумме двух оставшихся углов треугольника, не смежных с этим внешним углом. Иными словами, (см. рис.): d=a+c.{\displaystyle d=a+c.}

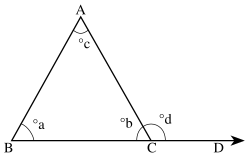Внешним углом DCA плоского треугольника ABC при данной вершине C называется угол, смежный внутреннему углу ACB треугольника при этой вершине

Доказательство (в обозначениях рис. выше)[править | править код]

Утверждение теоремы следует из теоремы о сумме углов треугольника, равной 180°.

Пусть ABC — произвольный треугольник с внешним углом d. Так как углы b и d — смежные, то их сумма равна 180°, то есть угол d = 180° — b. По теореме о сумме углов треугольника, угол b = 180° — (a + c). Из этого следует, что углы a + c = 180 — b. Так как d также равен 180 — b, то угол d = a + c. Что и требовалось доказать.

С другой стороны, если выполняется Теорема о внешнем угле треугольника, тогда справедливы следующая логическая цепь равенств:

d=a+c{\displaystyle d=a+c}

b+d=180∘=>{\displaystyle b+d=180^{\circ }=>}

b+a+c=180∘.{\displaystyle b+a+c=180^{\circ }.}.

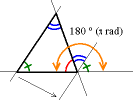Иллюстрация к евклидовому доказательству теоремы о внешнем угле треугольника

В евклидовом доказательстве теоремы о внешнем угле треугольника, принадлежащем Евклиду, (а также и результата о том, то сумма всех трех внутренних углов треугольника равна 180°) сначала проводится прямая, параллельна стороне AB, проходящая через вершину C, а затем, используя свойство соответственных углов при двух параллельных прямых и одной секущей и о внутренних накрест лежащих углах при двух параллельных прямых, требуемое утверждение получают как иллюстрацию (см. рис.).^[1].

Теорема о внешнем угле треугольника используется тогда, когда пытаются вычислить меры неизвестных углов в геометрии, в задачах с многоугольниками, где используются треугольники.

• Faber, Richard L. (1983), Foundations of Euclidean and Non-Euclidean Geometry, New York: Marcel Dekker, Inc., ISBN 0-8247-1748-1 
• Greenberg, Marvin Jay (1974), Euclidean and Non-Euclidean Geometries/Development and History, San Francisco: W.H. Freeman, ISBN 0-7167-0454-4 
• Heath, Thomas L. (англ.)русск.. The Thirteen Books of Euclid’s Elements (неопр.). — 2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925]. — New York: Dover Publications, 1956.

(3 vols.): ISBN 0-486-60088-2 (vol. 1), ISBN 0-486-60089-0 (vol. 2), ISBN 0-486-60090-4 (vol. 3).

• Henderson, David W. & Taimiņa, Daina (2005), Experiencing Geometry/Euclidean and Non-Euclidean with History (3rd ed.), Pearson/Prentice-Hall, ISBN 0-13-143748-8 
• Venema, Gerard A. (2006), Foundations of Geometry, Upper Saddle River, NJ: Pearson Prentice Hall, ISBN 0-13-143700-3 
• Wylie Jr., C.R. (1964), Foundations of Geometry, New York: McGraw-Hill 
• Wheater, Carolyn C. (2007), Homework Helpers: Geometry, Franklin Lakes, NJ: Career Press, с. 88–90, ISBN 978-1-56414-936-7 

Углы многоугольника. Сумма внешних и внутренних углов

Внутренний угол многоугольника – это угол, образованный двумя смежными сторонами многоугольника. Например, ∠ABC является внутренним углом.

Внешний угол многоугольника – это угол, образованный одной стороной многоугольника и продолжением другой стороны. Например, ∠LBC является внешним углом.

Количество углов многоугольника всегда равно количеству его сторон. Это относится и к внутренним углам и к внешним. Несмотря на то, что для каждой вершины многоугольника можно построить два равных внешних угла, из них всегда принимается во внимание только один. Следовательно, чтобы найти количество углов любого многоугольника, надо посчитать количество его сторон.

Сумма внутренних углов

Сумма внутренних углов выпуклого многоугольника равна произведению 180° и количеству сторон без двух.

s = 2d(n — 2)

где s – это сумма углов, 2d – два прямых угла (то есть 2 · 90 = 180°), а n – количество сторон.

Если мы проведём из вершины A многоугольника ABCDEF все возможные диагонали, то разделим его на треугольники, количество которых будет на два меньше, чем сторон многоугольника:

Следовательно, сумма углов многоугольника будет равна сумме углов всех получившихся треугольников. Так как сумма углов каждого треугольника равна 180° (2d), то сумма углов всех треугольников будет равна произведению 2d на их количество:

s = 2d(n — 2) = 180 · 4 = 720°

Из этой формулы следует, что сумма внутренних углов является постоянной величиной и зависит от количества сторон многоугольника.

Сумма внешних углов

Сумма внешних углов выпуклого многоугольника равна 360° (или 4d).

s = 4d

где s – это сумма внешних углов, 4d – четыре прямых угла (то есть 4 · 90 = 360°).

Сумма внешнего и внутреннего угла при каждой вершине многоугольника равна 180° (2d), так как они являются смежными углами. Например, ∠1 и ∠2:

Следовательно, если многоугольник имеет n сторон (и n вершин), то сумма внешних и внутренних углов при всех n вершинах будет равна 2dn. Чтобы из этой суммы 2dn получить только сумму внешних углов, надо из неё вычесть сумму внутренних углов, то есть 2d(n — 2):

s = 2dn — 2d(n — 2) = 2dn — 2dn + 4d = 4d

Внутренние односторонние углы | Треугольники

Еще один вид углов, образованных при пересечении двух прямых секущей — внутренние односторонние углы.

Две прямые разбивают плоскость на части. Та часть, которая лежит между прямыми — внутренняя. Углы, которые расположены в этой части, так и называются — внутренние. Внутренние односторонние углы — это углы, которые лежат внутри между прямыми по одну сторону от секущей (поэтому они так и называются).

При пересечении двух прямых секущей образуется две пары внутренних односторонних углов.

∠1 и∠2

∠3 и∠4

— внутренние односторонние углы при прямых a и b и секущей c.

 

Наибольший интерес вызывают внутренние накрест лежащие углы, образованные параллельными прямыми.

 

Свойство параллельных прямых

Если две параллельные прямые пересечены третьей прямой, то сумма внутренних односторонних углов равна 180º.

Если a ∥ b, то

∠1 +∠2 =180º

(как внутренние односторонние при  a ∥ b и секущей c).

 

Признак параллельных прямых

Если сумма внутренних односторонних углов равна 180º, то прямые параллельны.

∠3+∠4 =180º

А так как эти углы — внутренние односторонние при a и b и секущей c,

то a ∥ b (по признаку параллельных прямых).

 

Могут ли быть внутренние односторонние углы равны?

Да. Внутренние односторонние углы равны, если прямые параллельны, а секущая им перпендикулярна.

∠1  и ∠2 — внутренние односторонние углы при прямых a и b и секущей c

∠1 =∠2

тогда и только тогда, когда a ∥ b, а секущая c перпендикулярна и прямой a, и прямой b.

 

Внутренний угол Википедия

Тринадцатиугольник — многоугольник с 13 углами и 13 вершинами.

Многоуго́льник — геометрическая фигура, обычно определяемая как часть плоскости, ограниченная замкнутой ломаной, звенья которой не пересекаются.

Варианты определений

Многоугольники

Существуют три различных варианта определения многоугольника; последнее определение является наиболее распространённым.

• Плоская замкнутая ломаная — наиболее общий случай;
• Плоская замкнутая ломаная без самопересечений, любые два соседних звена которой не лежат на одной прямой;
• Часть плоскости, ограниченная замкнутой ломаной без самопересечений — плоский многоугольник; в этом случае сама ломаная называется контуром многоугольника.

В любом случае вершины ломаной называются вершинами многоугольника, а её звенья —

сторонами многоугольника.

Связанные определения

• Вершины многоугольника называются соседними, если они являются концами одной из его сторон.
• Стороны многоугольника называются смежными, если они прилегают к одной вершине.
• Отрезки, соединяющие несоседние вершины многоугольника, называются диагоналями.
• Углом (или внутренним углом) многоугольника при данной вершине называется угол, образованный его сторонами, сходящимися в этой вершине, и находящийся во внутренней области многоугольника. В частности, угол может превосходить 180°, если многоугольник невыпуклый.
• Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине. В общем случае внешний угол — разность между 180° и внутренним углом, он может принимать значения от −180° до 180°.

Виды многоугольников

Многоугольник, вписанный в окружность Многоугольник, описанный около окружности

• Выпуклый многоугольник это многоугольник, который лежит по одну сторону от любой прямой, содержащей его сторону (то есть продолжения сторон многоугольника не пересекают других его сторон). Существуют и другие эквивалентные определения выпуклого многоугольника.
• Выпуклый многоугольник называется правильным, если у него равны все стороны и все углы, например равносторонний треугольник, квадрат и правильный пятиугольник.
• Многоугольник, у которого равны все стороны и все углы, но который имеет самопересечения, называется правильным звёздчатым многоугольником, например, пентаграмма и октаграмма.
• Многоугольник называется вписанным в окружность, если все его вершины лежат на одной окружности.
• Многоугольник называется описанным около окружности, если все его стороны касаются некоторой окружности.

Свойства

• Сумма внутренних углов плоского n{\displaystyle n}-угольника без самопересечений равна (n−2)⋅180∘{\displaystyle (n-2)\cdot 180^{\circ }}.
• Число диагоналей всякого n{\displaystyle n}-угольника равно n⋅(n−3)2{\displaystyle {\tfrac {n\cdot (n-3)}{2}}}.

Площадь

• Пусть {(Xi,Yi)},i=1,2,…,n{\displaystyle \{(X_{i},Y_{i})\},i=1,2,…,n} — последовательность координат соседних друг другу вершин n{\displaystyle n}-угольника без самопересечений . Тогда его площадь вычисляется по формуле Гаусса:

S=12|∑i=1n(Xi+Xi+1)(Yi−Yi+1)|{\displaystyle S={\frac {1}{2}}\left|\sum \limits _{i=1}^{n}(X_{i}+X_{i+1})(Y_{i}-Y_{i+1})\right|}, где (Xn+1,Yn+1)=(X1,Y1){\displaystyle (X_{n+1},Y_{n+1})=(X_{1},Y_{1})}.

Квадрируемость фигур

С помощью множества многоугольников определяется квадрируемость и площадь произвольной фигуры на плоскости. Фигура F{\displaystyle F} называется квадрируемой, если для любого ε>0{\displaystyle \varepsilon >0} существует пара многоугольников P{\displaystyle P} и Q{\displaystyle Q}, такие что P⊂F⊂Q{\displaystyle P\subset F\subset Q} и S(Q)−S(P)<ε{\displaystyle S(Q)-S(P)<\varepsilon }, где S(P){\displaystyle S(P)} обозначает площадь P{\displaystyle P}.

Вариации и обобщения

• Многогранник — обобщение многоугольника в размерности три, замкнутая поверхность, составленная из многоугольников, или тело, ей ограниченное.

Многоугольники
Звёздчатые многоугольники
Паркеты на плоскости
Правильные многогранники и сферические паркеты
Многогранники Кеплера — Пуансо
Соты
Четырёхмерные многогранники	{3,3,3} {4,3,3} {3,3,4} {3,4,3} {5,3,3} {3,3,5}

Предложения со словосочетанием ВНУТРЕННИЕ УГЛЫ

Где надо по теореме про внешний и внутренний угол на круге… Нам в старой школе этого, кажется, не давали… Примером может служить хотя бы мигательный рефлекс: будучи крайне полезен для глаз вообще, так как с помощью его частицы пыли удаляются со слизистых оболочек к внутреннему углу глаза, тот же рефлекс может оказаться и крайне вредным, если какой-либо острый предмет попадёт под верхнее веко, ибо при мигании в этом случае возможно тяжёлое повреждение роговицы глаза. Имеются и другие характерные признаки заболевания: небольшой рост, коренастая фигура, искривлённые пальцы, толстый язык, маленький нос и кожные складки у внутренних углов глаз, что создаёт впечатление раскосых глаз. Раскосые глаза расширяются к внутреннему углу, к внешнему они немного сужаются. Внутренний угол глаза ниже внешнего, который тянется к краю надбровных дуг. Начинай не от внутреннего угла, а от середины века или из первой трети.

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: псевдонаучный — это что-то нейтральное, положительное или отрицательное?

Положительное

Отрицательное

Расстояние между глазами равно длине глаза, а его внешние и внутренние углы расположены на одном уровне. Добавлю, что ко всем этим видам отделки прилагаются специальные детали, предназначенные для сочленений наружных и внутренних углов. Они широко раскрыты, не сужаются к внутреннему углу глаз. Начинается у внутреннего угла глаза, затем поднимается через лобную и теменную области параллельно средней линии головы, которая проводится от внутреннего угла глаза. Ещё один шпатель понадобится для обработки внутренних углов. У внутреннего угла глаза, когда средние пальцы достигнут бровей, присоедини к ним средние или безымянные пальцы и продолжай поглаживать по краю верхнего века к височным ямкам, как бы зажимая брови между пальцами (рис. По-разному располагаются и оси глаз — условные прямые, которые проходят через наружный и внутренний углы глаза. Но удивительнее всего были глаза — водянистые, дымно-мутные, подёрнутые во внутренних углах красной паутинкой вен. При проверке наружного угла угольник накладывают на деталь его внутренней частью, а при проверке внутреннего угла — наружной частью. Отечественная промышленность для массового жилищного строительства предлагает электротехнический плинтус ПЭ-75, изготовленный из пожаробезопасной пластмассы трёх цветов и комплектуемый переходными коробками, внешними и внутренними углами и компенсаторами. Мышцы (кроме нижней косой и орбитальной) берут начало от соединительно-тканного кольца, окружающего зрительное отверстие, а нижняя косая — от внутреннего угла глазницы. Эти линии идут от середины лба к вискам, от внутреннего угла глаза по верхнему веку к наружному углу, по нижнему веку к внутреннему углу, от ноздрей к вискам, от угла рта к уху, от середины подбородка к мочке уха. Поглаживание век выполняйте по нижнему веку к внутреннему углу глаза и обратно — по верхнему веку, а массаж круговых мышц глаз, как и массаж век, — только в обратном направлении. Бывает разрез глаз, слегка напоминающий миндалевидный тем, что внешний и внутренний углы глаза расположены на одном уровне, к которым и сужаются глаза. Лёгкая гуннская конница была расположена в двух внутренних углах, образованных поперечными траншеями и рвом, с задачей, если тяжёлая конница на флангах будет отброшена назад, уменьшить давление на неё ударами в тыл атакующему противнику. WSI и WSII имеют важное фенотипическое различие: WSI характеризуется наличием dystopia conthorum (то есть латерального смещения внутреннего угла глаза, в наибольшей степени влияющей на их фенотип), в то время как WSII характеризуется его отсутствием. Напоминает пятиконечную звезду с отломанными кончиками, сколы ещё и по внутренним углам и в середине. Из внутренних углов звездообразной головы тянутся красноватые трубки длиной чуть больше желтоватых. Тут уже объяснения подсматривания «в щёлочки возле внутренних углов глаз» недостаточно. Расстояние же между внутренними углами глаз обращает на себя особое внимание, когда оно значительно приближается к ширине носа или даже превосходит её. Это будет внутренний угол. Затем, не отрывая рук, необходимо поместить указательные пальцы на симметричные точки меридиана мочевого пузыря цуань-чжу (V2), находящиеся у начала брови, над внутренними углами глаз, применяя приём чжэн-дин-фа. Большие пальцы рук спускаются по наружному краю трапецевидных мышц и, несколько расходясь, достигают внутренних углов лопатки. Сварка по внутреннему углу. На портрете, во внутреннем углу рамы, помещалась дощечка, на которой в нескольких словах была изложена вся история этого милого создания. Они способны не только параллельно сдвигаться, но и поворачиваться вокруг внутреннего угла рамы. Некоторые морфологические особенности, такие как плоско-лицесть, эпикантус (особая складка у внутреннего угла глаза) и другие, вошли в состав монголоидного комплекса расовых признаков. В каждую из вершин пентаграммы я поместил по куску завёрнутого в полотно хлеба, а в пяти внутренних углах её — пять открытых кувшинчиков с водой, которой наносил водяной круг. По внутренним углам стола на высоких стойках, поднимающихся из ваз с розами, установлены четыре канделябра со свечами, дополнительно освещающими стол. Опиливают наружные плоские и криволинейные поверхности, наружние и внутренние углы, фасонные поверхности, углубления, отверстия, пазы, выступы, кромки деталей (с целью снятия заусенцев). Доски нижней, цокольной, коробки жёстко соединяют брусками во внутренних углах, изнутри приклеивают опорные бруски. З — ножовочные напильники служат для опиливания внутренних углов клиновидных канавок, узких пазов, плоскостей в трёхгранных, квадратных и прямоугольных отверстиях, а также при изготовлении режущих инструментов и штампов. Однако, учитывая, что пустоты и вкладыши уменьшают несущую способность стен, их не следует устраивать в углах, при пересечении наружных стен с внутренними, в местах оконных и дверных проёмов ближе чем на 0, 4 — 0, 5 м от внутреннего угла стены или грани проёма, а также ближе чем на 10 см к вертикальной плоскости стены и 10 — 15 см друг к другу. Внутренние углы и дверные проёмы были аккуратно выложены из крупных блоков кубической формы, хорошо отёсанных по фасаду. Здесь можно выделить веки (верхнее и нижнее), ресницы, внутренний угол глаза со слёзным мясцом (складка слизистой оболочки), белую часть глазного яблока — склеру, которая покрыта прозрачной слизистой оболочкой — конъюнктивой, прозрачную часть — роговицу, через которую видны круглый зрачок и радужка (индивидуально окрашенная, с неповторимым рисунком). Во внутреннем углу глаза, на верхнем и нижнем веке, расположены слёзные точки — отверстия, через которые слеза по носослезному каналу оттекает в полость носа. В области внутреннего угла глаза слеза скапливается, образуя так называемое слёзное озерце, на дне которого виден слёзный сосочек. Обе части фиброзной оболочки хорошо видны невооружённым глазом (в центре глазной щели — роговица, в наружном и внутреннем углах — белочная оболочка). В раннем детском возрасте (от 0 до 5 лет) наиболее близко к пазухе и к внутреннему углу глазницы расположен клык. — Надо знать всем, у каждой собаки три века: верхнее, нижнее и боковое, оно спрятано во внутреннем углу глаза. Два верхних ряда выкладывают так же, как и нижние, — кирпич к кирпичу, чтобы кирпичи в нём внутренними углами касались друг друга. Необходимо следить за тем, чтобы просверливаемые в поперечных перекладинах отверстия находились от внутреннего угла профиля угловой стойки на таком расстоянии, которое не будет затруднять монтаж. Отступ от внутреннего угла профиля нужно делать не менее 6 мм, что позволит правильно смонтировать боковые детали (поперечины и листовые детали). Каждое платоново тело содержит так называемый двугранный угол, который является внутренним углом между двумя гранями.

Неточные совпадения

Непосредственно перед массажем на лицо наносится питательный крем, который распределяют лёгкими поглаживающими, не сдвигающими кожу движениями, подушечками второго, третьего и четвёртого пальцев обеих рук от середины лба к вискам, от основания носа к ушам, от середины подбородка к мочке уха, от наружного угла глаза — к внутреннему по нижнему веку и наоборот — по верхнему. Угольники применяются для проверки наружных и внутренних прямых углов. На уровне 4 — 5 грудных позвонков проток смещается влево, выходит на шею и впадает в левый венозный угол, образованный соединением подключичной и внутренней яремной вен. Для слесарной обработки внутренних прямых углов у шаблонов, калибров и лекальных инструментов применяют раздвижные угольники. Затем массажист воздействует на левую лопатку, начиная массаж I пальцем правой кисти от прикрепления широчайшей мышцы спины, доходит по наружному краю до нижнего угла левой лопатки и продолжает растирать пальцами со II по V по внутреннему краю лопатки и до затылка. Она покрывает голосовую мышцу, которая натянута между внутренней поверхностью угла щитовидного хряща спереди и голосовым отростком черпаловидного хряща сзади. В наружном углу стенки выявляется углубление для слёзной железы, а у места перехода верхней стенки во внутреннюю определяется выемка или отверстие для верхнеорбитальной вены и артерии. Для этого нужно определить по плану места углов бани и мест, где наружные стены будут стыковаться с внутренними. Внутренний и внешний углы у них расположены на одном уровне. Продвинувшись ещё немного в глубь подворотни, я успела заметить нескольких подозрительного вида подростков и услышать часть их диалога, но едва высунула голову из-за угла, чтобы повнимательнее рассмотреть внутренний двор и его обитателей, как тотчас же получила оглушающий удар по затылку и потеряла сознание. Там, напротив, царят покой и умиротворение: в каменных галереях — прохладный ветерок, по углам внутреннего сада — раскидистые розовые кусты, вот только рядом с каждым, как бы в напоминание о национальном темпераменте, — облупленная фанерная табличка: «Розы не рвать». У них внешний угол глаза ниже внутреннего, крупное верхнее веко. Кроме естественных разрушений, на нижних углах внутренней стороны лопасти сделано два пробных «раскрытия», результатом которых стали потёртости орнамента, написанного синей краской, и утрата белильных элементов росписи. Далее особо выделить ту лопатку, которая подвержена рефлекторному изменению и дифференцированно воздействовать с проникновением на определённые области лопатки, соответствующие данной патологии (так, левая лопатка, её нижний край, внутренняя часть, — при заболевании сердца, при патологии желудка — угол левой лопатки с проникновением в слои под ним, при заболевании печени — воздействовать на правую лопатку, её нижний угол, и по ости лопатки кнаружи к плечевому суставу). Картинки ложились на внутреннюю поверхность его обзорного стекла, автоматически искривляясь по углу зрения так, что ни одна из схем не выглядела изогнутой или напухшей. Для сохранения общего архитектурного вида здания существуют панели для внутренних и внешних углов, обрамление оконных и дверных проёмов. Было так темно, что когда ворота открылись, и мы въехали во внутренний двор, мы смогли разглядеть только силуэт высокого дома с крутою крышей, выделявшийся на фоне темнеющего неба, и группку людей с лошадьми в ближайшем к нам углу двора. Камни необходимо уложить под всеми углами конструкции, а также в местах, где должны находиться сочленения внутренних и наружных стен. Машина выехала из-за угла здания, где располагались ворота внутреннего двора, уже через пару минут… Но прямой угол может быть образован только с внутренними планетами. При установке плинтусов наибольшие трудности представляют углы помещения, как внутренние, так и внешние (последние относятся по большей части к коридорам и прихожим). Обноски ставятся на расстоянии не менее 1, 5 м от наружных граней стен здания, причём можно расположить их часто, по всему периметру дома, или прерывисто — в углах и месте устройства внутренних стен. Прежде всего, это армировочная лента для проклейки внутренних и внешних углов, стыков листов гипсокартона. Я ласкал их внутренним зрением, оглаживал их края, углы, малейшие выступы; сквозь бумажные полиграфические покровы пальцы мои чувствовали сухое, чуть пыльное дыхание материала. Грани бриллианта должны иметь такие углы наклона, чтобы наибольшее количество лучей света, упавших на бриллиант, претерпевало в нём полное внутреннее отражение. Внутренне убранство не блещет роскошью: тёмный большой ковёр на полу, циновки в человеческий рост — кровати, рядом лежат валики, набитые пухом, в дальнем углу на низком табурете стоит ларь для хранения ценных вещей. Где-то в дальнем углу комнаты мерно тикали часы, приводя и её внутреннее состояние к гармонии. Резьба имеет следующие основные элементы: шаг резьбы, угол профиля резьбы, глубина резьбы, наружный, средний и внутренний диаметры резьбы. В том месте, куда он указывал, виднелись маленькие гвоздики, вбитые под углом с внутренней стороны рамы: они удерживали холст в нужном положении. Неподвижные газетчики на углах, без выкриков, без движений, неуклюже приросшие к тротуарам, узкие пролётки с маленькой откидной скамеечкой для третьего, и, одно к одному, — девяностые годы слагаются в моём представлении из картин разорванных, но внутренне связанных тихим убожеством и болезненной, обречённой провинциальностью умирающей жизни.