Математика и архитектура — Википедия

Как и в других искусствах, в архитектуре используют математику по нескольким причинам. Даже если отбросить необходимость математики для проектирования здания, архитекторы используют геометрию для определения пространственной формы здания. Начиная со времён пифагореизма (VI в. до н. э.) для создания пространственных форм предполагалась гармония, а потому предполагалось проектирование зданий и их окружения согласно математическим, эстетическим и, иногда, религиозным принципам. Математику используют также для облицовки зданий с помощью математических объектов, таких как замощения, а также для достижения экологических целей, таких как минимизация скорости ветра около основания высотных зданий.

В Древнем Египте, Древней Греции, Индии и исламском мире здания, включая пирамиды, храмы, мечети, дворцы и мавзолеи, были спроектированы со специфичными пропорциями по религиозным причинам^[3][4]. В исламской архитектуре геометрические формы и геометрические мозаичные орнаменты^[en] использовали для облицовки зданий как внутри, так и снаружи^[5][6]. Некоторые индусские дворцы имеют подобные фракталам структуры, в которых часть имеет сходство с целым, передавая сообщение о бесконечности в индуистской космологии^[2][7]. В архитектуре Китая тулоу в провинции Фуцзянь — это круглые структуры коллективной защиты. В двадцать первом веке математические орнаменты снова начали использоваться для облицовки общественных зданий^{[8][9][10][11]}.

В архитектуре Возрождения симметрия и пропорции преднамеренно подчёркивались архитекторами, как это делали Леон Баттиста Альберти, Себастьяно Серлио и Андреа Палладио, находящиеся под влиянием трактата

Десять книг об архитектуре Витрувия, жившем в Древнем Риме, и арифметики пифагорейцев, религиозно-философского учения Древней Греции^[12]. В конце девятнадцатого века Владимир Шухов в России и Антонио Гауди в Барселоне положили начало использованию гиперболоидных конструкций^[13][14][15]. В Храме Святого Семейства Гауди также использовал гиперболические параболоиды, мозаики, арки с очертанием обратной цепной линии^[en], катеноиды, геликоиды и линейчатые поверхности^[13][14][15]. В двадцатом веке, стили, такие как архитектурный модернизм и деконструктивизм исследовали различные геометрии для получения желаемого эффекта^[16][17]. Минимальные поверхности используются в виде похожих на палатки крыш, как в Денверском Международном аэропорте. Ричард Бакминстер Фуллер положил начало применению усиленных тонкостенных оболочек, известных как геодезические купола ^[18].

Архитекторы Майкл Освальд и Ким Уильямс, рассматривая связь архитектуры и математики, заметили, что по общему пониманию эти две области связаны слабо, поскольку архитектура относится к практическому строительству зданий, в то время как математика является чистой теорией, изучающей числа и другие абстрактные объекты^[19]. Но, как они утверждают, эти две области сильно связаны и связаны они ещё с античности. В Древнем Риме Витрувий описывал архитектора как человека, знающего достаточно большой объём других дисциплин, главным образом геометрию, что позволяет ему контролировать квалифицированных ремесленников в других сферах деятельности, таких как каменщики и плотники^[20]. То же самое относится к средним векам, когда выпускники высших заведений учили арифметику, геометрию и эстетику наравне с базовыми курсами грамматики, логики и риторики (тривиум) в элегантных аудиториях, сделанных строителями, которые руководили многими рабочими.

[источник не указан 326 дней] Строителям на вершине их профессии давался титул архитектора или инженера. В эпоху Возрождения, квадривиум арифметики, геометрии, музыки и астрономии стал дополнительной программой, которую должны были знать люди эпохи Возрождения, такие как Леон Баттиста Альберти. Аналогично в Англии, сэр Кристофер Рен, сегодня известный как архитектор, был первоначально заметным астрономом^[21].

Уильям и Оствальд, рассматривая позднее взаимодействие математики и архитектуры с 1500 согласно подходу немецкого социолога Теодора Адорно, определили три тенденции архитектуры, а именно — революционная, предлагающая полностью новые идеи, реакционная, противящаяся нововведениям, и художники, возрождающие традиции^[en], на самом деле идущие назад^[22]. утверждали, что архитекторы избегали использование математики для получения вдохновения во времена возрождения традиций. Это может объяснить, почему во времена возрождения традиций, таким как неоготика в 19-м веке в Англии архитектура имела малую связь с математикой. Также они заметили, что во времена реакции, такие как итальянский маньеризм примерно с 1520 по 1580, или барокко и палладианство 17-го века, математика мало принималась во внимание. Для контраста, революционные движения ранних годов 20-го века, такие как футуризм и конструктивизм активно отбрасывали старые идеи, использовали математику и вели к модернизму в архитектуре. К концу 20-го века фрактальная геометрия была быстро подхвачена архитекторами, как и непериодичные замощения, позволяющие осуществить интересные и привлекательные облицовки зданий

[8].

Архитекторы используют математику по нескольким причинам, если даже оставить в стороне необходимость использования математики в проектировании зданий^[en][23]. Во-первых, они используют геометрию, поскольку она определяет пространственные формы здания

[24]. Во-вторых, они используют математику для проектирования форм, считающихся прекрасными или гармоничными^[25]. Со времён пифагореизма с их религиозной философией чисел^[26], архитекторы Древней Греции, Древнего Рима, исламского мира и итальянского Ренессанса выбрали пропорции строительного окружения — зданий и их окружения — согласно эстетическим и религиозным принципам^{[12][27][28][5]}. В третьих, они могут использовать математические объекты, такие как замощения, для украшения зданий^[29][30]. В четвёртых, они могут использовать математику в виде компьютерного моделирования для достижения экологических целей, таких как минимизация вихрей при огибании основания высоких здания ^[1].

Светская эстетика[править | править код]

Древний Рим[править | править код]

Витрувий[править | править код]

Подробное рассмотрение темы: Витрувий, Виртувианов модуль, и Десять книг об архитектуре

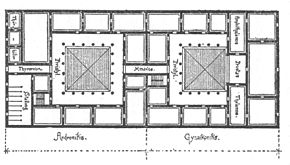
Влиятельный древний римский архитектор Витрувий утверждал, что планирование здания, такого как храм, зависит от двух качеств, пропорций и симметрии. Пропорции обеспечивают, чтобы каждая часть здания соотносилась гармонично с остальными частями. Симметрия в понимании Витрувия означает нечто более близкое к модульности, чем к зеркальной симметрии, так как это относится к сборке (модульных) частей в единое строение. В его базилике в городе Фано он использовал отношения малых целых чисел, в частности, треугольных чисел (1, 3, 6, 10, …) как пропорции структуры (виртувиановых) модулей^[en][a]. Так, ширина базилики относится к длине как 1:2, нефы вокруг неё имеют такую же высоту, как и ширину, 1:1, толщина колонн составляет пять футов, а высота — пятьдесят футов, 1:10^[12].

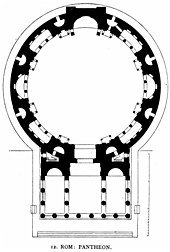План Пантеона

Витрувий назвал три свойства, требуемые от архитектуры в трактате Десять книг об архитектуре (15 век до нашей эры) — прочность, практичность и приятный вид. Эти свойства можно использовать как категории для классификации способов использования математики в архитектуре. Прочность охватывает использование математики для обеспечения устойчивости зданий, поскольку математические средства используются для проектирования и поддержки конструкций, например, для обеспечения стабильности и для качественного моделирования. Практичность достигается отчасти путём эффективного применения математики, обосновывая и анализируя пространственные и другие связи при проектировании. Приятный вид является атрибутом здания, получающимся воплощением математических связей в здании. Он включает эстетику, чувственные и интеллектуальные свойства^[32].

Пантеон[править | править код]

Сохранившийся невредимым Пантеон в Риме иллюстрирует классическую структуру римских строений, пропорции и украшение. Основной структурой является купол, высшая точка которого оставлялась открытой в качестве круглого окулюса, пропускающего свет. Пантеон с фасада снабжён колоннадой с треугольным фронтоном. Высота окулюса и диаметр внутреннего круга совпадают, 43,3 м, так что полностью внутренняя часть помещается в куб

[33]. Эти размеры будут более понятны, если обратить внимание на список древнеримских единиц — купол имеет диаметр 150 римских футов^[en]*[b]). Окулюс равен 30 римским футам в диаметре, дверной проём имеет высоту 40 римских футов^[34]. Пантеон остаётся крупнейшим в мире бетонным сводом без арматуры^[35].

Возрождение[править | править код]

Подробное рассмотрение темы: Архитектура Возрождения

Первым трактатом эпохи возрождения по архитектуре был трактат Леона Баттиста Альберти (1450)

On the Art of Building^[en] (Об искусстве строительства). Трактат стал первой печатной книгой по архитектуре в 1485. Трактат частично базировался на книге Витрувия Десять книг об архитектуре и, через Никомаха, пифагоровой арифметике. Альберти начинает с куба и выводит из него пропорции. Так, диагонали грани дают отношение 1:√2, а диаметр сферы, описанный вокруг куба имеет отношение 1:√3^[36][37]. Альберто также описывает открытие Филиппо Брунеллески линейной перспективы^[en], разработанной для планирования зданий, которые выглядят вполне пропорционально, если рассматривать с удобного расстояния^[5].

Следующим важным текстом была книга Себастьяна Серлио Regole generali d’architettura (Основные правила архитектуры). Первый том книги вышел в Венеции в 1537. Том 1545-го года (книги 1 и 2) охватывают геометрию и перспективу^[en]. Два метода Серлио построения перспективы были ошибочными, но это не остановило широкое использование книги

[39].

В 1570 Андреа Палладио опубликовал авторитетные I quattro libri dell’architettura (Четыре книги об архитектуре) в Венеции. Эти книги получили широкое распространение и распространяли идеи итальянского возрождения на остальную Европу в содействии со сторонниками идей, такими как английский дипломат Генри Уоттон, выпустивший в 1624 Элементы архитектуры^[40]. Пропорции каждого помещения внутри особняка вычислялись с помощью простых математических отношений, таких как 3:4 и 4:5, и различные помещения внутри дома были связаны этими соотношениями. Ранние архитекторы использовали эти формулы для балансирования симметрии фасада. Однако, проекты Палладио относились, как правило, к квадратным особнякам^[41]. Палладио допускал ряд отношений в Quattro libri, утверждая^[42][43]:

Имеется семь типов помещений, наиболее прекрасных и хорошо пропорциональных. Это круглые, хотя они редки, квадратные или их длина равна диагонали квадрата ширины, ширине с третью, ширине с половиной, ширине и две трети и две ширины.[c]

В 1615-м году Винченцо Скамоцци опубликовал в позднее Возрождение трактат L’Idea dell’Architettura Universale (Идея Универсальной Архитектуры)^[44]. Он попытался соотнести планирование городов и зданий с идеями Витрувия и пифагореан и более свежих идей Палладио^[45].

Девятнадцатый век[править | править код]

Гиперболоидные конструкции начали использоваться с конца девятнадцатого века Владимиром Шуховым для мачт, маяков и градирен. Их поразительные формы как эстетически интересны, так и крепки, при этом используют материал экономно. Первая гиперболоидная башня Шухова была представлена на выставке в Нижнем Новгороде в 1896^[46][47][48].

Двадцатый век[править | править код]

Подробное рассмотрение темы: Архитектурный модернизм и Aрхитектура 21-го века

Общество художников Де Стейл — заходящие друг за друга и пересекающиеся плоскости — Дом Шрёдер, 1924

В движении начала двадцатого века «архитектурный модернизм», у истоков которого лежал русский ^[d]конструктивизм^[49], использовалась евклидова геометрия. В движении общества художников Де Стейл горизонталь и вертикаль рассматриваются как составляющие вселенной. Архитектурные формы заключаются в помещении этих двух направлений вместе с использованием плоскости крыш, плоскостей стен и балконов, которые либо заходят одна за другую, либо пересекаются, как в доме Шрёдер 1924-го года Геррита Ритвельда^[50].

Архитекторы модернизма были свободны в использовании кривых наравне с плоскостями. Станция лондонской подземки в Арнос Гроув^[en] Чарльза Холден 1933-го года имеет круглый кирпичный кассовый зал с плоским бетонным полом^[51]. В 1938-м году художник из высшей школы строительства и художественного конструирования Баухаус Ласло Мохой-Надь заимствовал семь биотехнических элементов Рауля Генриха Франсе^[en], а именно, кристалл, сфера, конус, плоскость, (кубовидная) лента, (цилиндрический) стержень и спираль в качестве базовых строительных архитектурных блоков, навеянных природой^[52][53].

Ле Корбюзье предложил антропометрический масштаб пропорций в архитектуре «модулор», систему пропорций, основанную на высоте человека^[54]. В церкви Нотр-Дам-дю-О (Ле Корбюзье, 1955) используются кривые произвольной формы, не описываемые математическими формулами^[e]. Конструкция имеет только большие масштабы — нет иерархии меньших масштабов, а потому никаких фрактальных размерностей. То же самое имеет место для других знаменитых зданий двадцатого века, таких как Сиднейский оперный театр, Денверский Международный аэропорт и Музей Гуггенхейма в Бильбао^[16].

Мнения об архитектуре 21-го века^[en] 90 ведущих архитекторов, которые участвовали в опросе о мировой архитектуре^[en] 2010-го года, крайне расходятся. Лучшим считается Музей Гуггенхейма в Бильбао Фрэнка Гери^[55].

Здание терминала Международного аэропорта Дэнвера, построенного в 1995, имеет тканевую крышу^[en] поддерживаемую в состоянии минимальной поверхности (то есть её средняя кривизна равна нулю) стальными тросами. Здание напоминает снежные вершины Колорадо и палатки типи коренных народов США (часто их неверно называют вигвамами)^[56].

Архитектор Ричард Бакминстер Фуллер известен созданием крепких тонкостенных структур известных как геодезические купола. Купол Биосферы в Монреале имеет высоту 61 м, а его диаметр равен 76м^[18].

Сиднейский оперный театр имеет крышу, состоящую из взмывающих белых сводов, напоминающих паруса корабля. Чтобы сделать возможным построение из стандартных компонентов, своды составлены из треугольных секций сферической оболочки одинакового радиуса. Это требовало соблюдения одинаковой кривизны в любом направлении^[57].

Движение конца двадцатого века деконструктивизм создаёт обдуманный беспорядок, который Никос Салингарос в книге A Theory of Architecture (Теория архитектуры) называет случайными формами^[58] высокой сложности^[59]. Беспорядок создаётся непараллельными стенами, наложенными решётками и сложными двумерными поверхностями, как в концертном зале имени Уолта Диснея (архитектор Фрэнк Гери) и музее Гуггенхейма в Бильбао^[60][61]. До двадцатого века студенты архитектурных институтов обязаны были изучать основы математики. Салингарос утверждает, что первый «чрезвычайно упрощённый, политически мотивированый» модернизм, а затем «антинаучный» деконструктивизм эффективно отделили архитектуру от математики. Он убеждён, что эта «отмена математических значений» губительна, так как «повсеместная эстетика» нематематической архитектуры ведёт людей «к отказу от математической информации в окружающей среде города». Он утверждает, что это имеет негативный эффект на общество^[16].

Религиозные принципы[править | править код]

Древний Египет[править | править код]

Подробное рассмотрение темы: Древнеегипетские погребальные обряды

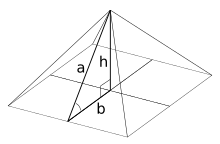
Пирамиды Древнего Египта были погребениями, построенными с преднамеренно выбранными пропорциями, но каковы они были, ведутся споры. Лицевой угол составляет около 51°85’ и отношение наклонной высоты на середину основания равно 1,619, что на 1 % меньше золотого сечения. Если это был метод расчёта, из этого следовало бы использование треугольника Кеплера (угол 51°49’)^[62][63]. Однако, более вероятно, что наклон пирамиды выбирался исходя из треугольника 3-4-5^[en] (угол 53°8’), известного из папируса Ахмеса (1650—1550 до нашей эры), или из треугольника, отношение основания которого к гипотенузе составляет 1:4/π (угол 51°50’)^[64].

Часто констатируется использование треугольника 3-4-5 для построения прямых углов, например для планирования основания пирамиды, и подразумеваемое знание теоремы Пифагора ^[3]. Сначала это предположил историк Мориц Бенедикт Кантор в 1882^[3]. Известно, что прямые углы были построены в древнем Египте точно^[3], что землемеры того времени использовали верёвки с узлами^[en] для измерения ^[3], что Плутарх записал в сочинении Об Исиде и Осирисе (около 100 года нашей эры), что египтяне восторгались треугольником 3-4-5^[3], и что берлинский папирус^[en] из Среднего царства (до 1700 года до нашей эры) утверждает, что «квадрат, имеющий площадь 100, имеет ту же площадь, что и два меньших квадрата. Сторона одного равна ½ + ¼ стороне другого.»^[4]. Историк математики Роджер Л. Кук заметил: «Трудно представить кого-либо, заинтересованного в таких вещах и не знающих теорему Пифагора.» ^[3]. Однако, Кук заметил, что ни в каком египетском тексте до 300-го года до нашей эры не упоминается использование теоремы для нахождения сторон треугольника и имеется более простой путь построения прямого угла. Кук заключает, что предположение Кантора остаётся сомнительным — он предположил, что древние египтяне, возможно, знали теорему Пифагора, но «нет свидетельств, что они использовали её для построения прямых углов»^[3].

Древняя Индия[править | править код]

Подробное рассмотрение темы: Индийская архитектура и Васту-шастра

Наука Васту-шастра, правила архитектуры и планирования городов древней Индии, использовала симметричное рисование, называемое мандала. Для определения размеров зданий и их компонентов использовались сложные вычисления. Планирование предполагало интеграцию архитектуры с природой, отдельных частей структуры и древних верований, использующих геометрические орнаменты (янтры), симметрию и размещение по направлениям^[en][65][66]. Однако ранние строители могли натолкнуться на математические пропорции случайно. Математик Джорж Ифрах заметил, что простые «хитрости» с верёвкой и колом могли быть использованы для разметки геометрических объектов, таких как эллипсы и прямые углы^[5][67].

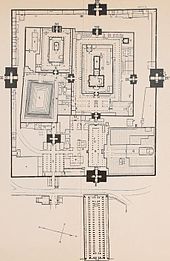
Математика фракталов использовалась для того, чтобы здания имели универсальную притягательность, поскольку они обеспечивали наблюдателю чувство масштаба с любого расстояния. Например, в высоких гопурамах индусских храмов, таких как Храм Вирупакши в Хампи, построенном в седьмом веке, и таких как храм Кандарья-Махадева в группе храмов Кхаджурахо^[en], у которых части и целое имеют одинаковые характеристики с фрактальной размерностью в границах от 1,7 до 1,8. Группа меньших башен (шикхара) вокруг более высокой центральной башни, которая представляет святую гору Кайлас, обиталище божества Шива, изображаемого в виде бесконечного повторения вселенных индуистской космологии^[2][7].

Храм Минакши в городе Мадурай является большим комплексом с множеством усыпальниц, с улицами, расходящимися концентрично от храма согласно Шастрам. Четверо ворот являются высокими башнями (гопурамы) с повторяющейся структурой, подобной фракталу. Участки вокруг каждого святилища прямоугольны и окружены высокими каменными стенами^[68].

Древняя греция[править | править код]

Подробное рассмотрение темы: Архитектура Древней Греции, Золотое сечение, Пифагореизм, и Евклидова геометрия

Архитрав — Википедия

Материал из Википедии — свободной энциклопедии

Архитрáв, или эпистелион (итал. architrave, от греч. ἀρχι, «архи», над-, главный и лат. trabs балка) — архитектурный термин, имеющий троякое значение.

Архитрав (итал. architrave, от греч. ἀρχι, «архи» — главный и лат. trabs — балка) — горизонтальная панель, опирающаяся на ряд опор, обычно это балочное перекрытие, поддерживающее верхнюю часть здания. В античности архитрав также называли эпистилем, так как обычно он опирался на колонны (греческое эпи-стиль означает «на колоннах»).

Архитрав распределяет нагрузку верхних архитектурных элементов, в частности, антаблемента, относящегося к конструкции крыши, на пилонах или колоннах, но также может встречаться и на завершении стены.

Различают архитравы монолитные и многорядные, в которых несколько блоков лежат один за другим. При определении размеров блоков архитрава архитектура подошла к пределам технически возможного. Например, средний элемент архитрава храма Артемиды Эфесской весил около 24 тонн, и его приходилось поднимать с помощью шкивов на высоту более 20 метров.

Архитрав встречается в египетской архитектуре, архитектуре Передней Азии и архаической Греции, а также во всех архитектурных стилях, использующих наследие античной архитектуры, в качестве поддерживающего или чисто декоративного элемента.

В зависимости от архитектурного стиля использовались всё новые и новые варианты архитрава. Прежде всего для дорического и ионийского ордера в греческой архитектуре были разработаны различные формы, которые впоследствии также использовались для коринфского ордера. С другой стороны, римская архитектура лишь слегка модифицировала греческие формы архитрава.

Дорический архитрав обычно гладкий и сверху увенчан выдвинутой вперед полочкой, называемой тения. На выступающей нижней стороне тении расположены повторяющиеся планки, регулы, с которых свисают конические каплевидные элементы — гутты. Классическое число этих элементов — шесть, но даже в раннем дорическом каменном зодчестве встречаются также варианты с четырьмя гуттами. Регулы расположены так, что каждая соответствует триглифу дорического триглифического фриза. Хотя внешняя часть архитрава обычно бывала гладкой, существуют исключения, когда архитрав несёт на себе фигурные рельефы, к примеру, храм Афины в Ассосе.

Первоначально очень массивные и высокие архитравы дорической архитектуры по мере развития становятся более плоскими и в архитектуре классического периода сокращаются приблизительно до двух третей нижнего диаметра колонны по высоте. В римской архитектуре дорический архитрав может редуцироваться до одной только плоской плиты.

В ионическом и коринфском ордере архитрав также может быть гладким, но обычно имеет две или — в классическом варианте — три горизонтальные полосы, так называемые фасции. В зависимости от этого говорят о двух- или трехфасциевом архитраве; окна или двери, которые отделаны фасциями, также называют архитравоидальными. Каждая расположенная выше фасция архитрава слегка выступает по отношению к расположенной ниже. Верхний конец образует волнистый профиль, который обычно украшают шнуром из бисера или перлами. Даже в ионической архитектуре есть исключения из правила, согласно которому плоскость архитрава не должна быть украшена рельефами. Например, в архаическом храме Аполлона в Дидиме углы архитрава были украшены горгонами, по бокам от которых располагались львы. Тем не менее ранний ионийский храм не знал фриза как отдельного архитектурного элемента, на котором могли бы размещаться такого рода рельефы.

Начиная с эпохи эллинизма, нижняя сторона (софит) ионийских архитравов и в особенности архитравов строений коринфского ордера могла быть украшена простыми круглыми элементами или цветочным орнаментом. Увлеченность декором, характерная для архитекторов и строителей поздней Республики и Принципата, перешла также на фасции, переходы которых стали покрываться волновыми профилями, такими как лесбосские листики, и целыми последовательностями профилей.

Облом (архитектура) — Википедия

Материал из Википедии — свободной энциклопедии

У этого термина существуют и другие значения, см. Облом.

Обло́мы (от древнеславянского: лом, ломать, лама = яма или впадина) — протяжённые архитектурные элементы, различные по своему поперечному сечению — профилю, расположенные по горизонтали (на цоколях, в карнизах, междуэтажных поясах или тягах, базах колонн), иногда по наклонной (в карнизах фронтонов), кривой (архивольты арок, нервюры) или ломаной (обрамления порталов, окон) линии. Обломы, широко распространённые в ордерной архитектуре, служат для усиления архитектурного декора, образно-художественной выразительности тектонической основы здания.

Обломы впервые получили применение в Древней Греции, откуда были заимствованы зодчеством Древнего Рима, затем Возрождения и европейской архитектурой последующих эпох. В современной архитектуре для металлических, бетонных и деревянных элементов конструкций употребляется термин профили (переплёты остекления, обрамления и тяги на навесных стеновых панелях).

Классические архитектурные обломы делятся на прямолинейные и криволинейные:

К прямолинейным архитектурным обломам принадлежат полка и полочка (прямоугольные и трапециевидные выступы) и плинт (прямоугольная база колонны или выступ стены).

Криволинейные архитектурные обломы, в свою очередь, делятся на простые (очерченные из одного центра) и сложные (очерченные из двух центров).

К простым архитектурным обломам принадлежит вал, валик и четвертной вал (выпуклая половина или четверть круга) и выкружка (вогнутая четверть круга).

К сложным архитектурным обломам принадлежат: дорический киматий или «гусёк», ионический киматий или «каблучок». Соединение полки с валиком образует астрагал.

Типы обломов[править | править код]

По поперечному сечению выделяются следующие типы обломов (нумерация соответствует иллюстрации справа):

1. полочка (прямоугольное сечение). Для полочки, расположенной в пьедестале колонны, зачастую используется название плинт
2. полка (более широкое прямоугольное сечение)
3. валик или торус (полукруглое сечение)
4. вал или торус (более широкое полукруглое сечение)
5. четвертной вал (сечение в виде четверти окружности)
6. обратный четвертной вал
7. каблучок (сечение содержит выпуклую и вогнутую дуги с выпуклой дугой наверху). Используется в капителях и карнизах
8. обратный каблучок с выпуклой дугой внизу используется в базах колонн и цоколях
9. гусёк (очертание сечения составлено из двух дуг окружностей, образующих рукописную строчную букву Г (г))
10. обратный гусёк
11. выкружка
12. обратная выкружка
13. жёлоб (сечение содержит вогнутую часть окружности или кривой)
14. скоция
15. астрагал (сложный профиль, состоящий из валика и полочки)
16. полочка с выкружкой

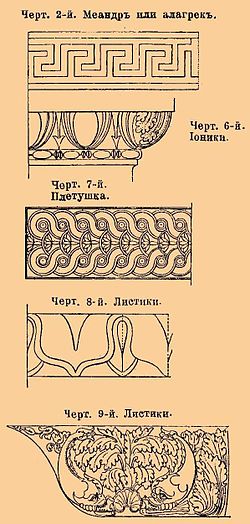Орнаменты для обломов

Прямолинейные обломы украшаются обычно геометрическим орнаментом, называемым порезкой, а криволинейные — органическим. Например, полки украшаются меандром; валики — шнуром из бисера или перлами, гуськи и каблучки — листиками, а четвертные валы — иониками. Порезки выполняются на обломах резьбой по камню или формовкой из гипса и других материалов.

Архитектурный ансамбль — Википедия

Материал из Википедии — свободной энциклопедии

Архитекту́рный анса́мбль (от фр. ensemble — целостность, связность, единство) — по определению БСЭ, «гармоническое единство пространственной композиции зданий, инженерных сооружений (мосты, набережные и др.), произведений монументальной живописи, скульптуры и садово-паркового искусства»^[1]. Образ архитектурного ансамбля зависит от смены освещения, времени года, присутствия людей. Важным элементом ансамбля может служить ландшафт. При этом ключевую роль может играть рельеф местности (например, церкви, которые строились на высоком берегу Волги). Очень часто архитектурные ансамбли включают водоёмы.

Архитектурные ансамбли возникают при условии единого пространственного решения комплекса.

Существуют архитектурные ансамбли, созданные единовременно, по единому плану и ансамбли, складывающиеся годами, усилиями многих зодчих, бережно дополняющих складывающуюся композицию так, что новые элементы органически сочетаются со старыми. Классическими примерами таких ансамблей могут служить Площадь святого Марка в Венеции и Дворцовая площадь в Санкт-Петербурге.

Часто в композицию архитектурного ансамбля включаются не только здания и элементы ландшафта, но и скульптуры, памятники. Примером таких ансамблей могут служить Сенатская площадь с фигурой Медного всадника и Исаакиевская площадь с памятником Николаю I (Санкт-Петербург).

Некоторые типы архитектурных ансамблей[править | править код]